今天对分布式系统领域的一篇经典论文 —— Chandy-Lamport 算法做了一下总结，这篇论文对于分布式快照算法产生了非常巨大的影响，比如：Apache Flink、Apache Spark 的 Structured Streaming、Ray 等分布式计算引擎都是使用的这个算法做快照。这篇论文的其中一位作者 —— Lamport，他也是 Paxos 算法的提出者，2013 年图领奖得主（图领奖是计算机领域的诺贝尔奖，目前只有一位华裔 —— 姚期智院士获得过这个殊荣，没错，就是清华交叉学院姚班的姚院士）。这篇论文发表于 1985 年，算法的由来可以参考下面的小段子：

The distributed snapshot algorithm described here came about when I visited Chandy, who was then at the University of Texas in Austin. He posed the problem to me over dinner, but we had both had too much wine to think about it right then. The next morning, in the shower, I came up with the solution. When I arrived at Chandy’s office, he was waiting for me with the same solution.

另外，如果你只是想要明白这个算法是怎么做的，可以直接看这篇文章 —— 分布式快照算法: Chandy-Lamport 算法，它讲得更通俗易懂，本文更多的是论文的角度来讲述，会详细介绍一下这个算法的数学证明。

背景 & 问题

分布式系统的很多问题都可以归结于获取 global states 的问题，比如：

1. stable property detection（系统的一些稳定特性检测），一个 stable property 是不可变的，如：计算停止或完成了（不会自己恢复的）、系统死锁了（不会自己恢复），通过 global states，就可以检测到这些 stable property；
2. 用于 checkpoint。

但是获取一个系统的 global states 并不是一件容易的事情，对于一个分布式系统而言，我们需要在同一个时间点记录下这个系统的全局状态，它包括每个 process 的状态以及相关 channel 的状态（一个计算是由有限的 process 和 channel 组成的一个 graph）。这就好比：在一个满是候鸟的天空大场景下，这个场景大到一张照片无法全部覆盖，摄影师不得不拍摄多张照片，然后把它们合并成一张全景，因为多张照片不能同时拍摄、在拍摄过程中候鸟也不会静止不动，所以如何保证合成的全景照片是有意义的（它可能少拍了某些鸟或者多拍了某些鸟）？这个就是分布式快照算法要解决的问题，因为没有全局统一的一把锁，所以不可能保证所有 process 能在同一时刻记录他们的状态信息。

分布式系统模型

一个分布式系统包含一个有限的 process 集合和有限的 channel 集合，它可以通过一个有向的 graph（顶点代表process、边代表 channel）来描述，如下图所示：

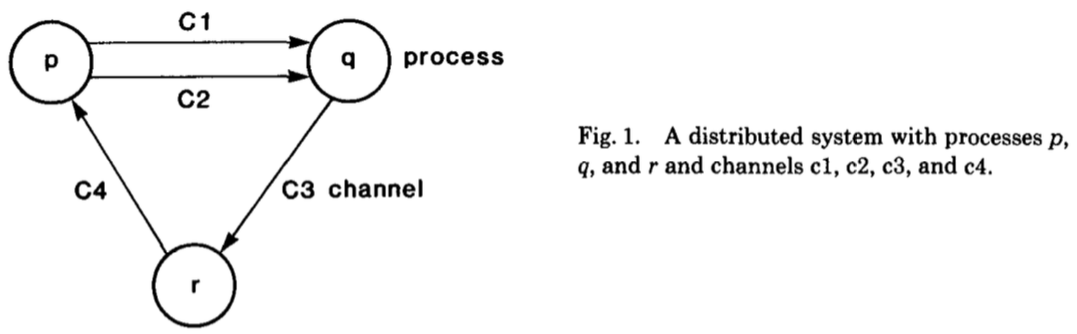
Channel：这里为了便于解释，文章会假设一个 channel 有一个无限、零错误、有序传输的 buffer（否者还要考虑 buffer 是否 full 的情况），channel 中数据的延迟是任意的并且有限的。一个 channel 的 state 就是它从上游收到的 msg list 减去下游已经接收到的 msg list；

Process：它是由一组状态、一个初始状态和一组 event 来定义。process p 中的一个 event e 代表一个可能改变 p 本身状态和对应 channel c 状态（c 发送或接收数据都可能会改变其状态）的原子操作。

一个 event e 被定义为 $<p, s, s’, M, c>$，其中：

1. Process p 是 event 产生的地方；
2. 在处理 e 之前 p 的状态是 s；
3. 在处理 e 之后 p 的状态是 $s’$；
4. Channel c 它的状态会被 e 所改变；
5. M 是发向或发离 c 的 msg；

如果 event 没有改变任何 channel 的状态，那么 M 和 c 则为 null，可能只改变了 p 的状态（这个概念很重要，需要好好理解，是后面论证的基础）。

global state 模型

有了前面的模型抽象，这里我们可以认为一个分布式系统的 global state 就是这批 process state 和 channel state 的集合。初始的 global state 就是每个 process 都是其对应的初始状态以及每个 channel 都是 empty 集合。

一个 event e 可能会改变 global state（这里记为 S），这里定义另外一个函数：$next(S, e)$，它指的是 event e 发生在 global state S 之后的 global state，根据前面介绍的，e 处理后的 global state 变化是：p 的状态由 s 变为 s'，Channel c 的状态是在原来的基础上加上（数据是发向 Channel c 的）或删除（数据是发离 Channel c 的） msg M。

这里再定义一个 $seq = (e_i: 0 \leq i \leq n)$，它代表的是这个分布式系统将要处理的 event 序列，这个 $seq$ 实际上就是 a computation of the system（这个 event 序列就代表了这个分布式计算），假设在 $e_i$ 处理前，系统的 global state 是 $S_i$（系统的初始状态时 $S_0$），那么可以得到下面公式：

$S_{i+1} = next(S_i, e_i)$, for $0 \leq i \leq n$

示例

论文中举了两个示例，这里也介绍一下，对于理解后面的论证是有帮助的。

Exmaple 1：Single-token Conservation

先看一个最简单的计算系统，这个系统有两个 process p 和 q，有两个 Channel c 和 c'（下面第二个示例也是这种基本模型），如下图所示：

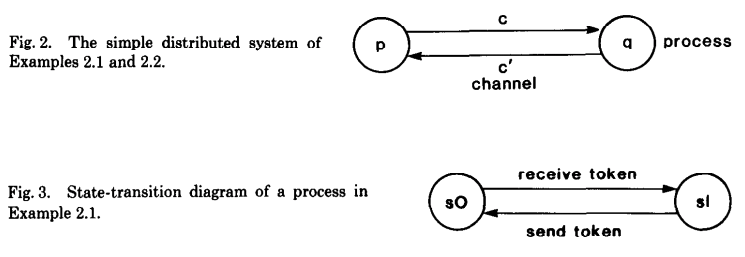
在这个系统中，有一个 token 它在两个 process 之间传输处理，每个 process 都有两种状态：$s_0$ 和 $s_1$，如果这个 process 不包含 token，它的状态就是 $s_0$，如果包含 token 的话，它的状态就是 $s_1$，p 的初始状态是 $s_1$，q 的初始状态是 $s_0$。而对每个 process 而言，都会有两种 event 类型（这里根据这个例子理解前面 event 的概念，如上面的图中所示）：

1. 发送 token 时，process 状态从 $s_1$ 转为 $s_0$；
2. 接收 token 时，process 状态从 $s_0$ 转为 $s_1$。

对于 global state 而言，可能会出现四种不同的状态，如下图所示：

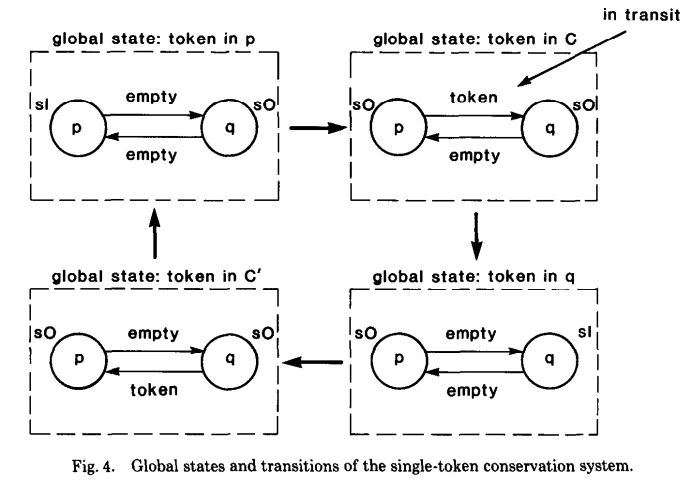
在上面图中，四种状态实际是跟 token 所在的位置有关：in-c，in-p、in-q、in-c'。这个示例比较简单，但它跟后面作者提出的算法来源的灵感有关。

Example 2: 非确定性计算

这里依然是两个 process p 和 q，它们的状态转移图如下所示：

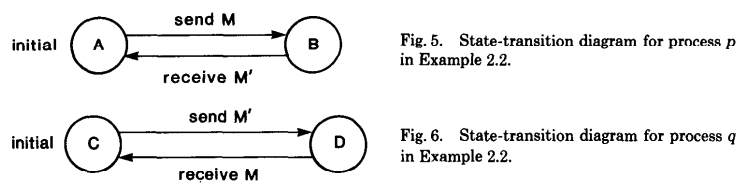
Example 1 的示例比较比较简单，在每个 global state 中正好只有一个 event（一个状态转换），但是在真实的系统中，很多情况下是一些非确定性计算（nondeterministic computation），可能同时会有多个 event 一起转换，比如：p 发送 M 和 q 发送 M' 这两个 event 同时发生（下面就是这两个 event 同时发生的情况，如下图的 global state $S_2$），那么得到的 global state 就会与预期的不同。下图是这个系统可能的一个 global state 转移情况：

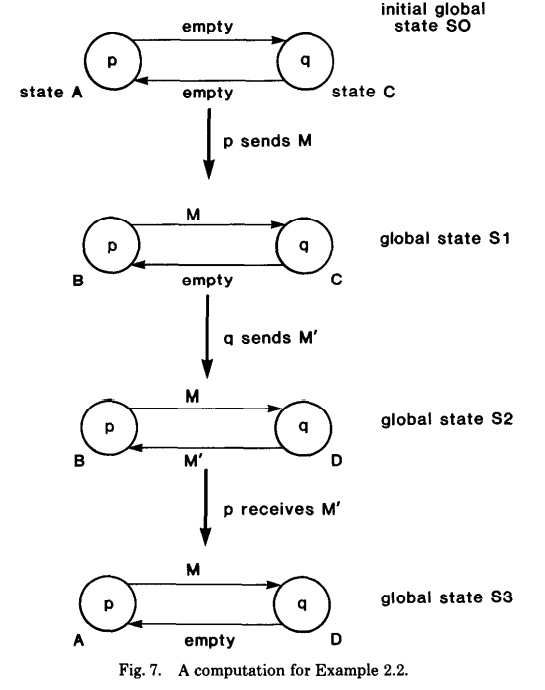
Notice： 这个示例，我在看的时候，最开始一直没有搞明白，主要在 $S_2$ 这一步没有明白，后来仔细想了几次，算是明白了，这个示例举得的是一个非确定计算的示例，上面也只是系统可能出现中的一种状态，比如：p 在发送 M 之后，M 在 Channel c 中还没有被 q 接收到，q 就发送了 M'。或者换成另一种理解方式，p 发送 M 和 q 发送 M' 同时发送，上图只是把两个拆开了一下展示，于是就有了 global state S1 和 S2，再接着有可能发生的就是 S3 的情况，p 接收到了 M'，状态发生了变化。这里，把这个示例当作一种在现实系统中的非确定性计算就好理解了。

Chandy-Lamport 算法

下面开始进入到算法的核心部分，这里作者介绍了一下算法的由来，以及在数学上的证明。

算法的动机/由来

Global state recording 算法工作过程如下：

• 每个 process 记录自己的 state；
• process 之间的通道 Channel 也会记录自己的状态；

因为没有一个全局的锁，所以我们无法保证，所有的 process 和 Channel 都是在同一时刻记录的。因此，我们需要保证记录的 process 和 Channel 状态能够组成 一个有意义的 global state。

这个算法是与跟底层计算嵌套在一起，但是不会对计算产生改变、也不会影响底层的计算。这里通过一个示例来逐步引出我们的算法，假设我们是可以很自然地记录 Channel 的状态，Channel c 是 process p 和 q 的之间的传输通道，下面来分析一下它们之间的状态关系。

p 与 c 状态之间的关系

这里以前面 Single-token Conservation 的示例来分析，假设 process p 的状态记录在 global state in-p 中，p 记录的状态显示 token 是在 p 中。现在假设 Channels c 和 c' 以及 process q 的状态时记录在 global state in-c 中的，同样 c 中记录的状态也显示 token 在 c 中（因为无法保证它们在同一时刻记录，所以每个组件是有可能在不同的时刻记录）。组成的 global state 显示系统中有两个 token，一个是在 p 中、一个是在 c中。但是由于这个系统是 single-token，它是不可能同时出现两个 token 的，所以一定是哪里有问题了，这样组成的 global state 不是有意义的。先定义两个变量：

1. $n$：在 p 的状态记录前，p 发往 Channel c 的 msg 数；
2. $n’$：在 c 的状态记录前，p 发往 Channel c 的 msg 数；

上面出现的情况就是 $n < n’$.

假设另一种情况，c 的状态记录在 in-p 中，而 p、q、c' 的状态记录在 in-c，那么这样组成的 global state 会显示系统没有 token，这个组成的 global state 同样也是没有意义的，这就是 $n > n’$ 的情况。

从前面的分析中，可以得到：这里有个一致的全局状态要求

$n = n’$

q 与 c 状态之间的关系

这里，再定义另外两个变量：

1. $m$：在 q 的状态记录前，q 从 Channel c 中接收到的 msg 数；
2. $m’$：在 c 的状态记录前，q 从 Channel c 中接收到的 msg 数；

跟前面的分析类似，这里也会有一个一致性的要求：

$m = m’$

分析

在任何一种状态下，都要求 Channel c 下游接收到的 msg 数不能超过 p 发送给 Channel 的 msg 条数，即：

$n’ \geq m’$ 以及 $n \geq m$

现在来分析一下 Channel 的状态要记录什么数据？ 一个 Channel 要记录的状态是，它 sender 记录自己状态之前它所接收到的 msg 列表，再减去 receiver 记录自己状态之前它已经收到的 msg 列表，减去的之后的数据列表就是还在通道中的数据列表，这个列表是需要 Channel 作为状态记录下来的。而如果 $n’ = m’$，那么 Channel c 中要记录的 msg 列表就是 empty 列表。如果 $n’ > m’$，那么要记录的列表是 $(m’+1)st , … n’$ 对应的 msg 列表。

重点，重点，重点：分析到这里之后，就有了下面的一个灵感：那么 Channel c 状态要记录的 msg 列表是可以在 q 中记录的。那么具体怎么做的？就是在发送数据中插入一条特殊的数据 —— marker 数据，这条数据不会对计算有任何影响，那么 c 的状态就是 q 在记录自己状态之后并在收到 marker 之前接收到 msg 列表，另一种情况就是 q 收到 marker 之后，就必须要把自己的状态记录下来（伟大的算法就这样诞生了）。

算法概况

对于发送者来说：

• 在 p 记录自己的状态之后它先向 Channel c 发送一条 marker，然后才会继续发送数据信息；

对于接收者来说：

• 如果 q 已经还没记录自己的 state，在收到 marker 之后，它会记录自己的状态，并且把 c 的状态设置为 empty；
• 如果 q 已经记录自己的 state，它会把从 c 接收到的数据作为 msg 列表当作 c 的状态记录下来。

算法能够在有限时间结束的论证

关于算法能够在有限时间内结束，是有两个前提的：

1. marker 数据不会在 Channel 阻塞永远发不出去的；
2. Process 在根据一个初始状态记录自己的状态时，能够在有限的时间内完成。

有了这两个前提，一个 graph 中每个 process 都会收到相应的 marker，然后都会记录自己的状态，所以这个是完全可以保证能够在有限的时间内完成。

算法证明

事先说明，这里证明比较烧脑，我尽量描述清楚，最开始看论文也是看了好几遍、想好几遍把整个过程捋顺，当然如果理解有误，欢迎指正。

以前面 Example 2 的示例来讲述，假设在 global state $S_0$ 时，p 记录下了自己的状态（A），然后 p 向 Channel c 发送一条 marker 数据（它是在 M 数据之前），假设这个时候系统在正常运行，已经经历 $S_1$、$S_2$，到了 $S_3$ 阶段，但是 marker 数据在传输中。q 在收到 marker 之后，它记录了一下自己的状态 D（对应 c 的状态为空），然后再发送一条 marker 数据给 Channel c'。p 因为之前已经记录过自己的状态，所以在收到 c' 传过来的 M' 之后（p 先收到 M' 然后才会收到 q 发送的 marker 消息），会把它作为 Channel c' 的状态记录下来。

整个流程下来，组合的 global state 是 $S_*$，如下如所示：

可以看到这里算法得到的 global state $S_*$ 与真实环境下的 global state（$S_0$、$S_1$、$S_2$、$S_3$）都不相同。

那么来考虑一个问？题：如果算法记录的状态，在真实环境中并没有实际存在过？那么这个 global state 有什么用呢？（或许大家之前都理解了这个算法，但很少有人会去思考深入这个问题）

算法结论

假设 $seq = (e_i, 0 \leq i)$ 是一个分布式计算（是一个 computation），global state $S_i$ 是在 event $e_i$ 处理前系统当时的全局状态（这个是真实的那个时刻的状态）。假设算法在计算 global state 时是在 $S_t$ 时初始化，并且在 $S_ø$ 前终止的（算法在计算全局状态时会横跨多个 event），也就是 $0 \leq t \leq ø$，那么如果我们能证明下面的结论，基本上回答了上面的问题：

1. $S_*$ 可以由 $S_t$ 得到；
2. $S_ø$ 可以由 $S_*$ 得到；

如果能证明这个，那就说明，算法得到的 global state 是可以由之前的 global state 得到，并且得到后面的 global state，从工程上来理解就是，算法得到的 global state 是可以完整正确得恢复计算作业的状态信息，让作业继续运行。

前面的是结论，这里将证明转化为：存在一个序列 $seq’$，它可以满足以下条件：

1. $seq’$ 是 $seq$ 集合的一种变形（元素列表相同、顺序不同）， $S_t$、$S_*$、$S_ø$ 都是发生在这个 $seq’$ 上面的 global state；
2. $S_t$ 早于 $S_*$ 或者两者相等；
3. $S_*$ 早于 $S_ø$ 或者两者相等。

一个更加数学化的描述（方便后面证明）：一定存在一个 computation $seq’ = (e’_i, 0 \leq i)$，它满足以下条件：

1. 对于所有的 $i$，当 $i < t$ 或者 $i \geq ø$ 时，$e’_i = e_i$；
2. $e’_i(t \leq i < ø)$ 序列是 $e_i(t \leq i < ø)$ 序列的一种变换（元素相同，顺序可能会有不同）；
3. 对于所有的 $i$，当 $i \leq t$ 或者 $i \geq ø$ 时，$S’_i = S_i$；
4. 并且存在一个 $k, t \leq k \leq ø$，使得 $S_* = S’_k$；

这里实际要证明的是，找到这个 $seq’$，并且找到上面第四条要求的 $k$。

结论证明

为了证明上面的结论，这里引入两个概念：

1. prerecording event（后面记为 preEvent）：对于 process p 中的 event $e_i$，如果 p 做 snapshot（记录自己的状态）发生在收到 $e_i$ 之后，那么这个 $e_i$ 就是 prerecording event（也就是说：做 snapshot 时这个 $e_i$ 已经处理过了）；
2. postrecording event（后面记为 postEvent）：对于 process p 中的 event $e_i$，如果 p 做 snapshot（记录自己的状态）发生在收到 $e_i$ 之前，那么这个 $e_i$ 就是 postrecording event（也就是说：这个 $e_i$ 是在做完 snapshot 后才处理的）；

因此，对于 $e_i, (i < t)$，都是 preEvent，对于 $e_i, (i \geq ø)$，都是 postEvent。

对于一个真实的 computation，可能会出现一个 postEvent $e_{j-1}$ （$i < j < ø$）出现在 preEvent $e_j$ 之前，当然这种情况只可能是 $e_{j-1}$ 和 $e_j$ 出现在不同的节点上（大家可以反向思考一下：对于同一个节点来说，event 的处理会保证 FIFO，如果 $e_{j-1}$ 是 postEvent，那么 $e_j$ 必然也是 postEvent）。

接下来，我们证明一下下面的结论：

对于一个 event 序列 $seq’$（$seq$ 序列的变形），在这个序列中，所有的 preEvent 都在 postEvent 之前，下面我们将要证明 $S_*$ 就是 $seq’$ 中处理完所有 preEvent 后的 global state。

这里假设有一个 postEvent $e_{j-1}$ （$i < j < ø$）出现在 preEvent $e_j$ 之前，这里我们将证明 交换 $e_{j-1}$ 和 $e_j$ 的位置之后得到的新 $seq’$ 序列依然是一个 computation（与原来的计算是保持一致的，只不过在中间某些时刻它们当时的状态不完全相同）。根据前面的叙述，这里的 event $e_{j-1}$ 和 $e_j$ 肯定是在两个不同的 process 上的。这里假设 $e_{j-1}$ 发生在 p 上，$e_j$ 发生在 q 上。

首先经过分析可以得到：绝对不可能出现 $e_{j-1}$ 发送一条数据然后在 $e_j$ 中收到，通过反证法分析：

1. 如果当 $e_{j-1}$ 发生时，通过 Channel c 向 q 发送了一条数据，那么在发送数据前一定已经有了 marker 发送过去（因为 $e_{j-1}$ 是 postEvent）；
2. 当 $e_j$ 发生时，如果从 Channel c 中获得了这条数据，那么在这之前一定先收到了 marker 数据，这样的话，$e_j$ 也变成了 postEvent，所以这种情况是不可能存在的（这里不是很容易理解，可以换一种思路理解，它说明了 $e_{j-1}$ 和 $e_j$ 之间是没有因果关系的）。

因为 $e_{j-1}$ 是发生在 p 中的，所以当 $e_{j-1}$ 发生时，q 的状态是不会改变的（可以回顾一下前面关于 event 的公式定义）。而假如 event $e_j$ 触发时，q 会从 Channel c 收到一条数据 M，那么 M 一定是在 Channel c 中队列的头部，并且是在 $e_{j-1}$ 之前，因为 $e_{j-1}$ 发出的数据是不可能会在 $e_j$ 中接收到的。因此，$e_j$ 可以出现在 global state $S_{j-1}$ 中（这个可以在回顾一下前面关于 $S_j$ 的定义，实际这段说明了 $e_j$ 可以出现在 $e_{j-1}$ 之前，因此也就有了这个结论）。

而且在 $e_j$ 发生时，p 的状态并没有改变，因此，$e_{j-1}$ 是发生在 $e_j$ 之后的。那么也就是说明 $e_1, e_2, … , e_{j-2}, e_j, e_{j-1}$ 也是一个 computation，而且在经过这个 $e_1, e_2, …, e_{j-2}, e_j, e_{j-1}$ 计算之后的 global state 也跟 $e_1, e_2, …, e_{j-1}, e_j$ 计算之后的 global state 是一致的（主要还是因为 $e_{j-1}$ 和 $e_j$ 之间是没有因果关系的）。

假设 $seq^*$ 也是 $seq$ 的序列的一个变形，它只是把交换了 $e_{j-1}$ 和 $e_j$ 的位置，假设 $\overline{S_i}$ 是 $seq^*$ 对应的瞬时（就是当时那一刻系统的真实状态，i 对应的是序列第几个 event）全局状态，则有下面的公式：

$\overline{S_i} = S_i, i \neq j$

如果将前面的 postEvent 与后面紧贴的 preEvent 的位置互换，将会存在一个 $seq’$（$seq$ 序列的一个变形），使得：

1. 所有 preEvent 都在 postEvent 前面；
2. $seq’$ 是一个 computation（这个 computation，我理解它的意思是说这个变换后的序列列表依然是可以运行的计算逻辑）；
3. 当 $i < t$ 或者 $i \geq ø $ 有 $e’_i = e_i$；
4. 当 $i \leq t$ 或者 $i \geq ø $ 有 $S’_i = S_i$；

现在我们证明： 这个 $seq’$ 序列中所有 preEvent 处理完之后的 global state 就是 $S_*$ ，只需要证明下面两点即可：

1. $S_*$ 中的每个 p 的状态是与 p 处理完所有 preEvent 之后的状态相同的，这个并不用证明，因为 perEvent 的概念就是这样来的，它指的就是那些在 snapshot 前要处理的 event 列表；
2. $S_*$ 中的每个 Channel c 的状态：所有 preEvent 发往 c 的数据列表，减去所有 preEvent 从 c 接收到数据列表。

这里看下上面的第二点：假设 c 是 process p 和 q 之前的 Channel，$S_*$ 中关于 Channel c 的状态指的是，q 在记录自己的状态后在收到 marker 前从 c 收到的数据列表。而 c 在收到 marker 前接收到的数据列表都是 preEvent 发送过去的，所以上面第二点也就是完全得证了。

到这里，整个证明就结束了，我在看原论文的时候，这个证明看得云里雾里，看了好几遍才理解这个证明逻辑，这里比较关键的点有两个：

1. 前面所说的 $e_{j-1}$ 和 $e_j$ 之间是没有因果关系的，所以他们可以交换位置，并不会对后面的计算产生什么影响；
2. 算法得到的 global state，作者找到了理论上的解释，就是处理完 preEvent 之后系统那个时刻的状态，虽然现实系统并不一定有这个状态，但它是有意义的，它可以完整、正确得恢复系统的状态，让系统继续后面的运行，并且恢复后的系统后面的运行情况跟正常情况是保持一致的。

最后，作者给出了前面 Example 2 的解释，前面状态转移图中，发生的 event 事件列表如下：

1. $e_0$：p 发送 M，并且将状态转移成 B（这是一个 postEvent，在这之前 p 已经记录了自己的状态）；
2. $e_1$：q 发送 M'，并且将状态转移成 D（这是一个 preEvent，因为它发送在 q 记录自己状态之前，根据前面的讲述，因为 q 是 global state $S_3$ 时收到的 marker，当然这里只是其中一种情况，这里就是解释前面的所述的情况）；
3. $e_2$：p 接收到 M'，并且将状态转移成 A（这是一个 postEvent，以为在这之前 p 已经记录了自己的状态）。

根据上面的证明，这里的 $seq’$ 序列就是 $e_1、e_0、e_2$，而前面图中记录的 global state 就是系统在处理完 $e_1$ 之后的结果。

总结

这篇论文的思想还是比较容易理解的，比如 分布式快照算法: Chandy-Lamport 算法 这篇文章介绍得就很简洁清晰，在我前面的文章 Paper 阅读: Lightweight Asynchronous Snapshots for Distributed Dataflow 中也讲述了 Flink 是如何将这个算法在落地应用的，但是这个算法的证明，并不容易。在看这篇论文之前，我并没有想过这个算法应该怎么证明？因为我潜意识的认为这是一个很容易理解、很正确的算法，甚至感觉完全不需要证明，就像苹果就应该从树上落到地上一样。但是看完这篇论文之后，才不得不佩服 Lamport 大神的牛逼之处，它不但提出了这个算法，还给这个算法找到理论上的证明方法，虽然论文并不是那么容易理解，但看完看明白之后收获很大，再次向 Chandy 和 Lamport 致敬~

---

参考：

• Distributed Snapshots: Determining Global States of Distributed Systems；
• 分布式快照算法: Chandy-Lamport 算法；
• Distributed snapshot；
• 分布式Snapshot和Flink Checkpointing简介；